29 Nov Estimación de potencia en ciclistas profesionales: resumen del trabajo realizado por Ammatti Pyoraily y Thomas Wire

Ammatti Pyoraily y Thomas Wire publicaron recientemente en redes sociales un trabajo propio muy interesante que recopilaba datos de potencia de un gran número de corredores profesionales en ascensos (incluidas etapas de la Vuelta a España 2016). Con estos datos, los autores realizaron una comparación entre los datos reales (medidos con potenciómetro) y la estimación de la potencia basada en dos fórmulas matemáticas:

• Fórmula del Dr. Ferrari: W/kg = VAM / (100 x [2 + 0.1 x pendiente %]
• Fórmula de J. Martin et al.: W = drag aerodinámico + resistencia al rodamiento + gravedad

El presente blog es un resumen en español de los datos que mostraron originalmente los autores y que pueden encontrar en este enlace en su versión original: https://drive.google.com/file/d/0B9BaZuAbl3tRSXg0SHdXalFlNVk/view

Para los curiosos, los datos del trabajo se extrajeron de:

• 1252 subidas o “partes” de subidas (1000 de ellas de la última Vuelta a España) de entre 1.8 y 25.5 km con un 6-15% de pendiente media.
• 65 corredores profesionales diferentes (27 de ellos compitiendo en la Vuelta).
• Esfuerzos de 5 min a 1 h 35 min.
• Rango de potencia entre 225-482 W.

El primer análisis que Pyoraily y Wire realizaron fue comparar la potencia real de todas las subidas (medida con potenciómetro) y el resultado de las dos fórmulas mencionadas anteriormente, diferenciando tres CdA (drag aerodinámico) diferentes para la fórmula de Martin et al.:

	Real vs. Fórmula Dr. Ferrari	Real vs. Fórmula Martin et al. con CdA = 0.3500	Real vs. Fórmula Martin et al. con CdA = 0.3050	Real vs. Fórmula Martin et al. con CdA = 0.32625
Diferencia en %	1.86 ± 4.53 %	0.40 ± 2.96 %	-0.48 ± 2.79 %	-1.30 ± 2.69 %
Coeficiente de determinación	0.8726	0.9483	0.9549	0.9498

De esta tabla se extrajeron datos bastante claros: la fórmula de Martin et al. se ajusta mucho mejor a las medidas reales de potencia medidas en subidas y, dentro de esta fórmula, aquella con el CdA = 0.3050 dio el mejor coeficiente.

Además, en un análisis más detallado, los autores vieron como la fórmula de Martin et al. (CdA = 3050) mantuvo un grado de estimación muy preciso en todo el rango de potencia (desde 225 a > de 400 W), en todo el rango de % de pendiente de las subidas (desde 6-7 a >10 %) y en todos los rangos de tiempo (5-50 min) exceptuando aquellos esfuerzos mayores a 50 min debido a la mayor influencia del viento, cambios de peso, etc. Sin embargo, la fórmula del Dr. Ferrari, sobreestimaba siempre la potencia ante % de pendiente entre 6-9% y la subestimaba para valores mayores a 10%.

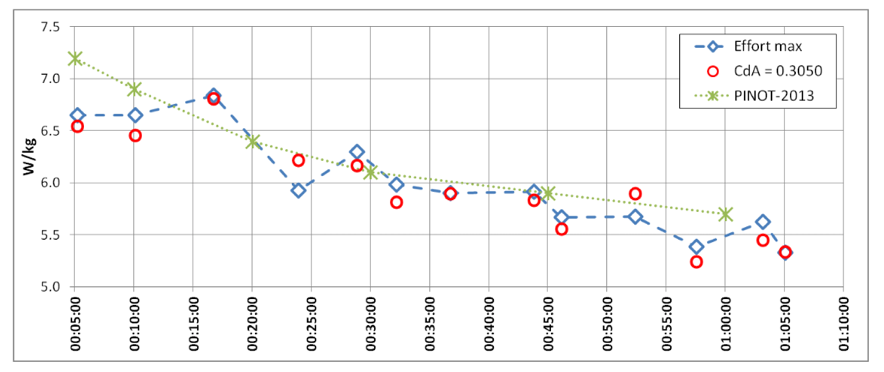
Por último, también muy interesante es “perfil de potencia genérico” que conformaron con los datos de potencia en función del tiempo. Este es el gráfico en cuestión:

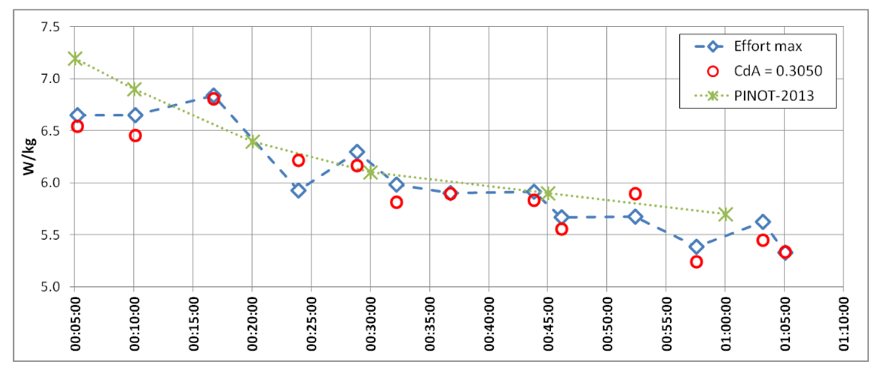
En él podemos ver tres líneas de datos:

• Verde: picos de potencia de Pinot (corredor profesional del TDJ)
• Azul: picos de potencia máxima (W/KG) en función del tiempo generado con los valores de potencia de todos los corredores.

Aunque el gráfico no permite conocer exactamente los valores en cada punto del perfil, si podemos hacernos una ligera idea de dónde se encontraría el nivel de un deportista que quisiera optar a pódium en una gran vuelta:

• P5 min ­~ 6.6 W/kg
• P10 min ~6.6 W/kg
• P17 min ~ 6.9 W/kg
• P30 min ~6.4 W/kg
• Etc.

Conclusiones:

• A la hora de estimar la potencia real en un ascenso ciclista, la fórmula desarrollada por Martin et al. es la mejor opción.
• Optaremos por un CdA = 3050 para conseguir el mejor coeficiente de determinación en ese cálculo.
• La fórmula ha demostrado ser bastante
  robusta, pero tiene limitaciones en esfuerzos mayores a 50 minutos.

REFERENCIAS BIBLIOGRÁFICAS

• Pyoraly
  & Wire (2016). Estimating climbing performances of professional cyclists: a
  larger dataset.
• J.Martin, D. Milliken, J. Cobb, K. McFadden and A.
  Coggan, Validation of a mathematical model for road cycling power, Journal of
  applied biomechanics, 1998, Vol. 14, 276-291.