27 Oct Factores Fisiológicos Determinantes del Rendimiento en Trail Running “Modelo Clásico de la Resistencia y Factores Específicos”
Desarrollaremos los determinantes del rendimiento del trail running estructurando un artículo presentado en dos partes del siguiente modo:
Parte 1: trail running “corto” (distancias hasta 42 km: categorías XXS y XS) y el modelo clásico de la resistencia
Parte 2: Ultra trail running.
Parte 1.
1. Trail running y el modelo clásico de la resistencia
Los predictores del rendimiento en las carreras de resistencia en calle, pista o en plano son ampliamente conocidos, esto es, el máximo consumo de oxígeno (VO2 máx.), umbral o fracción de utilización del VO2 y economía de carrera (RE) (Morgan et al., 1991; Joyner, 2008; Jones, 1998; Midgley et al., 2006), junto a factores psicológicos y motivacionales pero los factores o hitos determinantes no están claros para las carreras en entornos naturales (Bjorklund et al, 2019).
Las carreras de trail running más cortas y de ultra-trail implican correr distancias (extremadamente) largas en terrenos irregulares y accidentados con grandes cambios de elevaciones positivas y negativos (G. Millet 2011) e independientemente del formato de carrera, se han propuesto muy pocos modelos para caracterizar los determinantes del rendimiento (Lemire et al., 2020).
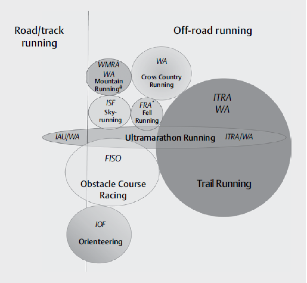
El trail running es la disciplina más popular de las carreras todoterreno, se define como una carrera a pie en un entorno natural que incluye montañas, desiertos, bosques, zonas costeras, selvas y selvas tropicales, llanuras áridas sobre una variedad de terrenos diferentes (por ejemplo, camino de tierra, sendero forestal, arena, etc.) con superficies asfaltadas mínimas (no deberían superar el 20-25% del recorrido total de la carrera) (V. Scheer 2020).
Figura 1. Clasificación de diferentes pruebas de running en calle, pista, y montaña. Datos de Scheer V. et al. (2020).
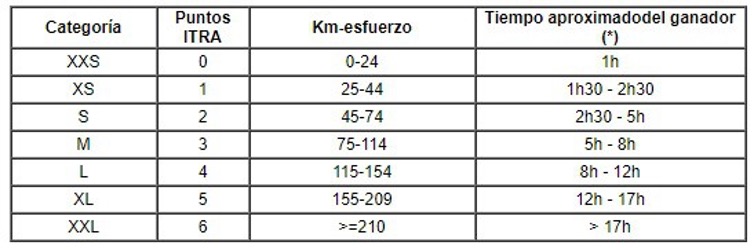
Para tener en cuenta tanto la distancia a recorrer como la diferencia de altitud, la clasificación de carreras utiliza el criterio de “Km-esfuerzo”, que se calcula sumando la distancia (en km) y la centésima de la ganancia de elevación positiva (en metros) (km-esfuerzo = distancia (km) + desnivel (m)/100. Los límites entre las categorías de senderos se han definido para que estos últimos reflejan mejor el esfuerzo que los atletas deberán realizar en una carrera. Esta nueva clasificación, implementada en marzo de 2018, tiene siete categorías de carreras de trail que van desde XXS a XXL (Tabla 1).
Tabla 1. Las siete categorías de carreras de trail definidas por la ITRA. (*) Tiempo estimado para un ganador a nivel internacional (índice de rendimiento ITRA de al menos 830).
1.2. Fisiología y biomecánica de la carrera en pendiente
Dewolf y col. (2016) demostró recientemente que el modelo mecánico clásico de resistencia difiere de la carrera en los segmentos de ascenso y descenso, y que durante la carrera cuesta arriba, el mecanismo de “rebote” desaparece gradualmente a medida que aumentan la velocidad y la pendiente. La energía elástica proveniente del tendón de Aquiles y la aponeurosis plantar aportan el 45% de la energía requerida en carrera plana (Snyder 2012); correr en pendientes positivas inhibe este mecanismo debido al desajuste en el almacenamiento de energía elástica durante el aterrizaje: requerimiento de mayor energía mecánica para superar la energía potencial asociada a la pendiente, demandando más actividad muscular para el trabajo positivo o concéntrico durante la fase de propulsión y compensar de esta forma la disminución de energía elástica (Gottschall JS., Kram R. 2005).
La carrera plana se caracteriza por un equilibrio entre las contracciones: las acciones musculares concéntricas y excéntricas (es decir, 50/50%). La contribución de la contracción de los músculos concéntricos aumenta con la inclinación de la pendiente creciente y, a la inversa, la contribución de la acción muscular de forma excéntrica aumenta con el creciente gradiente de pendiente negativa.
Una pendiente de ± 15% parece exacerbar estas modalidades excéntricas / concéntricas (en la carrera al -15%, casi el 80% del trabajo externo total proviene de trabajo externo negativo y por lo tanto acción muscular excéntrica, Minetti et al. 1994).
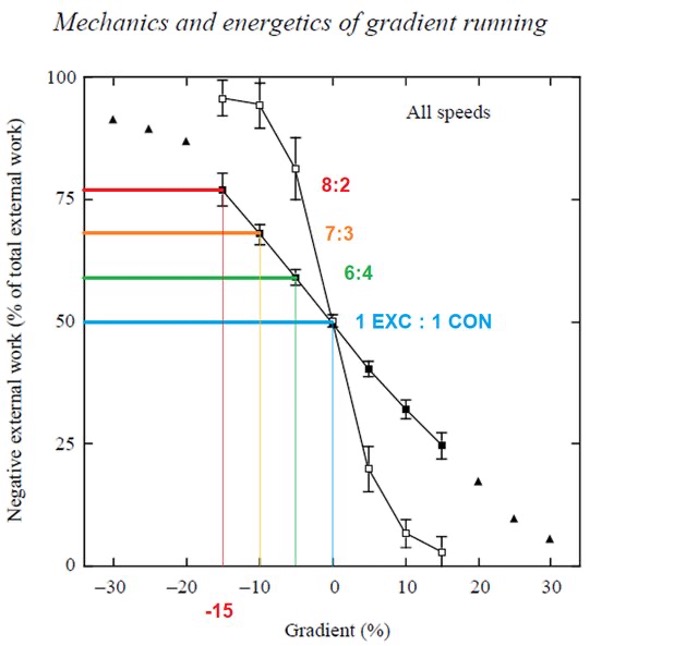
Figura 2. Porcentaje de trabajo negativo en función de la pendiente (adaptado de Minetti et al., 1994).
La carrera cuesta abajo se asocia con un mayor impacto y velocidad vertical superior durante la fase de apoyo, lo que resulta en una acción muscular excéntrico más fuerte de los músculos extensores de las extremidades inferiores (Figura 3).
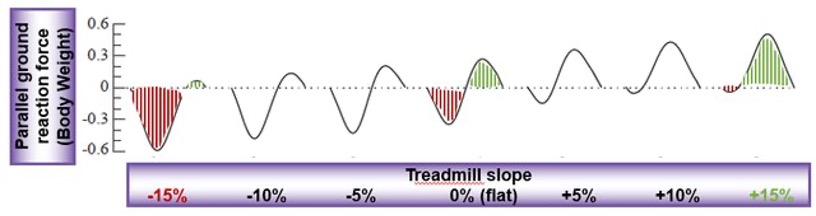
Figura 3. Cuanto más negativa es la pendiente, más importante es la acción muscular excéntrica (rojo) relacionada con el frenado en comparación con acción muscular concéntrica (verde), N = 10 (adaptado de Gottschall et al, 2005).
En la literatura sobre la locomoción de la carrera de ascenso y descenso surgen dos nociones de velocidad: velocidad horizontal (clásica) y velocidad vertical. La velocidad vertical refleja la velocidad de ascenso y caracteriza mejor la progresión en subida y bajada. Por lo tanto, la velocidades óptimas de marcha en gradiente (~ 25%), es decir, con el V̇O2 más bajo en comparación con la progresión vertical, las cuáles son aproximadamente 2,3 km/h con +0,6 km/h vertical en subida y unos 5,4 km/h con -1,3 km/h de descenso vertical. El gasto de energía vertical (Cvert) es entonces de 0,4 y 2,0 ml de oxígeno por kg de masa corporal y por metro vertical rebajado o elevado (Minetti, 1995).
El Cvert representa el gasto de energía para caminar o correr una distancia que corresponde a un desplazamiento vertical de 1 metro (Minetti et al., 2002). Se introdujo para centrarse en la optimización de los caminos de montaña (Minetti, 1995), teniendo esto en cuenta, es un índice más preciso para representar la cantidad de energía gastada para cubrir un camino inclinado. Con base en la literatura (ver Minetti et al., J Appl Physiol, 2002; Giovanelli et al., J Appl Physiol, 2016) hay un rango de gradiente donde Cvert tiene un mínimo. G. Vernillo destaca que, a pesar de la fatiga, Cvert estuvo en línea con la literatura: cuanto mayor es el gradiente, mayor es la Cvert (Vernillo, 2017). Pero, en conjunto, la literatura sugiere que existe un rango de gradientes para los cuales se minimiza el Cvert y, en consecuencia, cualquier esfuerzo realizado por encima o por debajo de este rango debería conducir a un gesto menos económico.
Por lo tanto, la aplicación práctica del conocimiento de este rango, es de funcionalidad en diferentes estrategias, como ejemplo: caminar y usar bastones cuando la pendiente del camino que está cubriendo un atleta está fuera de este rango.
1.2.1. Predictores de la carrera en pendiente
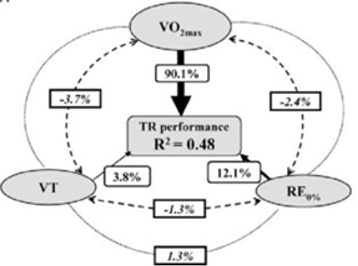
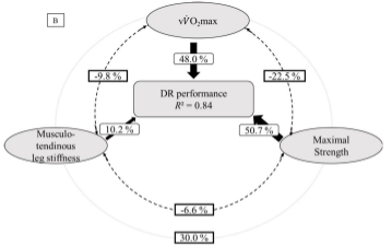
Ehrstrom et al. (2018) mostró la influencia del modelo fisiológico clásico de carrera de resistencia en un formato de carrera corta de trail running (27 km, 1200 metros de elevación positiva en el sudeste de Francia, realizada en diciembre de 2012); y reportó que el V̇O2 máx. representa el 90% del modelo explicativo, pero con una r² baja (es decir, r² = 0,48, Figura 4).
Figura 4. Representación gráfica de modelos de regresión para predecir el rendimiento de TR para el modelo clásico de carrera de resistencia. Datos de Ehrstrom (2018).
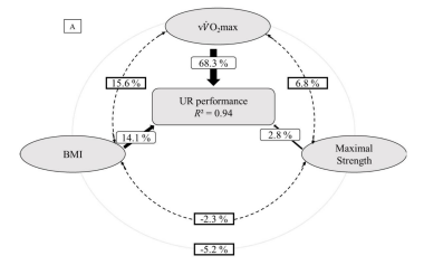
Sin embargo, el poder predictivo del modelo se mejoró notablemente al incorporar factores más específicos del TR, como la resistencia local o la economía de carrera (EC) medida en condición de pendiente positiva (Figura 5).
El TR implica el exigente desafío de correr cuesta arriba, donde los corredores deben superar la gravedad para elevar su masa corporal tan rápida y eficientemente como sea posible, por lo que no es sorprendente que el VO2 máx. relativo se muestre como un parámetro importante al correr en pendiente positiva y correr al aire libre (Staab et al., 1992; Townshend et al., 2010).
Es relevante destacar que el VO2 máx. es de menor importancia para el rendimiento de la carrera cuesta abajo, al aire libre como en condiciones de laboratorio (Townshend et al., 2010, Liefeldt et al., 1992; Staab et al., 1992; Minetti et al., 2002; Toyomura et al., 2018).
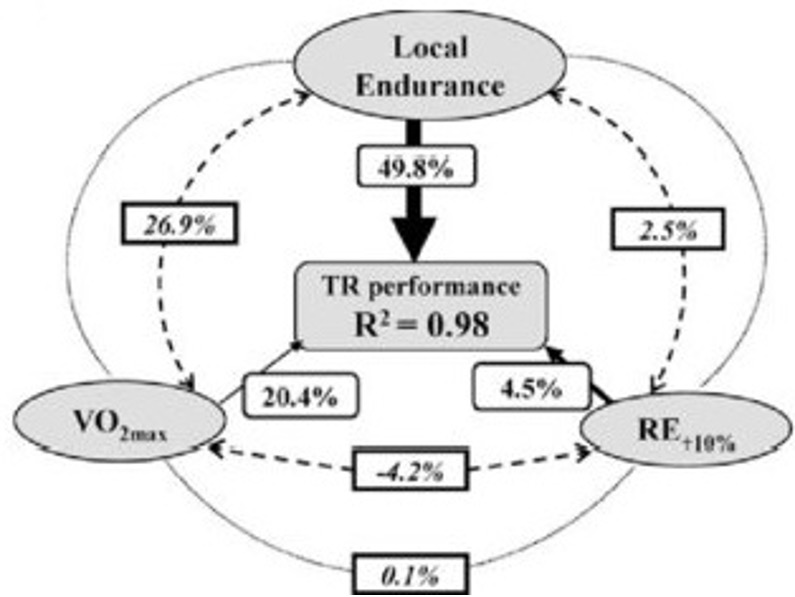
Figura 5. Análisis para el modelo adaptado y específico al TR (Ehrstrom et al. 2018).
1.2.2. Respuestas cardiorrespiratorias
La frecuencia cardíaca (FC) es menor en las carreras de descenso que en cuesta arriba, pero solo cuando esta comparación se realiza a la misma velocidad: tanto a 6,2 km/h como a 8,5 km/h (Pokora, Kempa, Chrapusta, & Langfort, 2014). Al comparar la respuesta cardíaca al correr cuesta abajo versus cuesta arriba con la misma intensidad metabólica (es decir, ~ 48 mL/kg/min) o con la intensidad máxima (es decir, prueba incremental máxima), entonces la FC es mayor o igual en cuesta abajo que cuesta arriba (Breiner, Ortiz, & Kram, 2018).
Al comparar las respuestas cardíacas, la FC y el pulso de O2 (11,9 frente a 24,8 mL/lat) fueron más bajos en la carrera cuesta abajo, lo que sugiere menos volumen sistólico y diferencia de O2 arteriovenoso durante la carrera, cuesta abajo frente a cuesta arriba (Dufour et al., 2004, Montgomery & Grabowski, 2018).
Cuando se prueban los esfuerzos máximos en una pendiente negativa, esto da como resultado que se alcance la FC máx., mientras que no se alcanza el VO2 máx. Esto sugiere que en la carrera cuesta abajo, una alta estimulación mecánica no está asociada con una alta respuesta metabólica.
Al escalar, el VO2 máx. se describe como determinante (Figura 6), limitado por el suministro de O2 a los músculos activos y, por tanto, por mecanismos centrales como gasto cardíaco, flujo sanguíneo muscular y concentración sanguínea arterial hemoglobina (di Prampero, 2003). Se sugiere que la velocidad en el máximo consumo de oxígeno (vV̇O2 máx.) cuesta arriba es por lo tanto determinada principalmente por la eficiencia de la función cardiorrespiratoria de los atletas, antes de su potencial de fuerza muscular (Balducci et al., 2016). La relación entre la fuerza de los músculos de las extremidades inferiores y el V̇O2 máx./vV̇O2 máx. no ha sido explorada hasta la fecha.
A una intensidad constante y moderada de carrera, el V̇O2 aumenta con el aumento de la pendiente positiva. Cuesta abajo, el V̇O2 disminuye al aumentar la pendiente negativa hasta -10%, parece que hay una meseta alrededor del -17% y finalmente, en pendientes más pronunciadas, el V̇O2 aumentaría.
Aparece un componente lento de V̇O2 para los esfuerzos intensos en la ejecución subir con pendientes > 10%. Al igual que la carrera plana, esto está asociado con muchos factores, principalmente la fatiga metabólica, la disminución de eficiencia y el reclutamiento de otras unidades motoras Tipo II.
Figura 6. Determinantes de la carrera en ascenso (M. Lemire 2020).
1.2.3. Fuerza muscular específica
En descenso, un alto potencial de fuerza muscular podría convertirse en un requisito previo para atletas para lograr altas velocidades de carrera (ver figura B, Lemire 2020) y, por lo tanto, altos valores de VO2 máx.
La carrera cuesta abajo es una acción muscular pliométrica, ya que los músculos solicitados (en particular gastrocnemio y sóleo) se someten a una fase excéntrico seguido de una fase concéntrica. Estirar estos músculos genera un reflejo miotático y la fascia también se estira.
García-Pinillos et al. (2018) originó una regresión lineal que destacó un vínculo entre la rigidez musculoesquelética-tendón y los parámetros cinemáticos de la zancada a diferentes grados de pendiente:
El componente vertical de la rigidez musculotendinosa se asoció con el contacto, tiempo de vuelo, frecuencia de carga aerodinámica, ángulo de zancada, pero no en la amplitud de la zancada.
Sin embargo, el trabajo de Björklund et al. (2019) sugiere que la fuerza requerida en la sección descendente es diferente al de la sección ascendente y muestran que las fuerzas máximas registradas gracias a los sensores en la suela son más importantes cuesta abajo que cuesta arriba (es decir, 1106 vs 959 N), mientras que los valores de impulso son mayores cuando se sube vs descenso (248 vs 175 N).
Algunos autores han buscado específicamente establecer la relación entre resistencia a la fuerza (por ejemplo, índice de fatiga de las extremidades inferiores) y una carrera de TR corto (27 km y desnivel 1200 metros de ascenso) han mostrado una fuerte correlación entre los dos (Ehrstrom et al., 2018). Basado en un análisis de regresión, la resistencia local representa de forma única el 49,8% del efecto total del rendimiento de un recorrido corto entre las tres variables en este modelo (es decir, VO2 máx., resistencia local y economía de carrera en una pendiente de + 10%).
En la tensión excéntrica de la contracción muscular, la fuerza generada por el músculo esquelético es insuficiente para superar la carga externa y las fibras musculares se alargan a pesar de su activación. Este es particularmente el caso de los extensores de los músculos de las extremidades inferiores durante actividades como caminar o correr cuesta abajo (Gottschall y Kram, 2005; Lienhard, Lauermann, et al., 2013). Durante el trabajo muscular excéntrico, los músculos consumen menos O2 y utilizan menos ATP que durante el trabajo muscular concéntrico realizado con la misma potencia mecánica (Curtin y Davies, 1973).
Figura 7. Determinantes de la carrera en descenso (M. Lemire 2020).
1.2.4. Carrera en pendiente negativa
Es común escuchar que “las carreras se ganan en subida y se pierden bajando”. Esta declaración parece más adecuada en ultra-trail, ya que un estudio realizado en el UTMB 2014, Gindre y Lussiana (2015) demostraron que los corredores mejor clasificados fueron aquellos para quienes observó una menor degradación de la velocidad de descenso durante el evento (-20% en promedio para corredores clasificados del 1 al 30 vs -40% para los corredores clasificados del 501 al 530).
Staab, Agnew y Siconolfi (1992) sugieren que el ritmo de descenso puede estar limitado por factores biomecánicos en lugar de factores fisiológicos, y Liefeldt, Noakes y Dennis (1992) identifican variables biomecánicas específicas de generación de fuerza alterada. Por lo tanto una carrera cuesta abajo exitosa requiere adaptación biomecánica, no solo para maximizar la velocidad sino también para evitar incurrir en daño muscular debido al mayor impacto y fuerzas de frenado implicadas en la carrera cuesta abajo (Gottschall y Kram, 2005).
En terrenos escarpados o accidentados existe más riesgo de lesiones por caídas, por lo que aparece un problema psicológico, requisito de valentía y el grado del riesgo asumido será producto de la “habilidad descendente” y la estrategia en competencia.
Townshend, Worringham y Stewart (2010) en pendientes comparativamente suaves
de descenso, se deben considerar otros factores de rendimiento, como la velocidad y la coordinación, puesto que a menudo se caracterizan por un exceso de velocidad que puede requerir un nuevo patrón motor. Además, las irregularidades del terreno, específicas de las carreras de trail, implican tanto un alto nivel de vigilancia y una mayor coordinación.
Las características antropométricas del corredor es un factor importante en el rendimiento cuando se trata de moverse en una superficie inclinada. Las fuerzas gravitacionales están directamente relacionadas con el tipo de pendiente (Gottschall & Kram, 2005) y son proporcionales a la masa del sujeto según la ley universal de gravitación.
En cuanto al corredor de montaña experto, no existe consenso sobre el carácter predictivo de la antropometría sobre el rendimiento de una carrera de montaña. Así, Fornasiero et al. (2018) muestran una asociación no significativa entre masa corporal, IMC y grasa corporal con la realización de un ultramaratón de montaña.
Sin embargo, Björklund et al. (2019) demostró que el rendimiento durante una repetición de dos contrarreloj de 3,5 km en terreno montañoso se correlacionó positivamente con la masa magra (o masa libre de grasa) y negativamente con el porcentaje de grasa corporal de los corredores entrenados.
2. Determinantes fisiológicos y biomecánicos del rendimiento en trail running de corta distancia (≤ formato S)
Los estudios de Ehrstrom (2018) se basaron en la identificación de determinantes fisiológicos de rendimiento en trail runing de corta distancia, con el fin de determinar un modelo de rendimiento específico a este tipo de prueba. El modelo teórico inicial se basó en el uso de los hitos fisiológicos del rendimiento establecidos en la carrera tradicional (p. ej., maratón) que incluye VO2 máx, % VO2 máx. en el umbral ventilatorio o umbral láctico y EC (Daniels y Daniels, 1992; Foster y Lucia, 2007; Joyner y Coyle, 2008; McLaughlin et al., 2010). Por tanto, McLaughlin et al. (2010) mostró que estas tres variables explicaron el 97,3% del rendimiento alcanzado durante una carrera de 16 km en ruta para corredoras y corredoras bien entrenados.
Las principales diferencias de la carrera de trail en comparación con la carrera tradicional son el terreno irregular y técnico, así como la sucesión de partes ascendentes y descendentes (con muy pocas porciones planas). Estas variaciones requieren una adaptación constante del sistema musculoesquelético que resulta en variaciones en la frecuencia de zancada, el nivel de activación muscular, las contracciones musculares (concéntrica o excéntrica), la intensidad de las fuerzas de propulsión y frenado en función de la pendiente y la velocidad de carrera (DeVita et al., 2008; Giandolini y col., 2016d; Gottschall y Kram, 2005c; Khassetarash et al., 2020; Vernillo y col., 2020a).
Por lo tanto, parecía necesario introducir variables más específicas en el modelo de rendimiento de TR. Así, los resultados del estudio mostraron que el modelo clásico de la resistencia en carreras solo explicó el 48,1% del rendimiento (no significativo) durante una competencia de TR en formato S para un grupo de competidores altamente capacitados. Por el contrario, la inclusión de parámetros específicos de la carrera por senderos de corta distancia, como la resistencia muscular (RM) y la economía de carrera cuesta arriba con una pendiente del 10% (EC10%), permitió obtener un modelo significativo (R2 = 0.98).
Estos resultados mostraron que los corredores con mayor RM (es decir, menor índice de fatiga) tuvo los mejores tiempos de carrera en la competencia. Aprovechando el trabajo realizado por Hayes y col. (2011) sobre la marcha plana, es probable que una mejor RM limite los cambios en reclutamiento muscular y / o coordinación, retrasando así la aparición de fatiga y degradación de la EC.
Recientemente, Noordhof y Sandbakk (2020) sugirieron que las variables deberían medirse después de un ejercicio submáximo prolongado para establecer un patrón de rendimiento relevante en eventos de larga distancia, destacando la importancia de la resistencia a la fatiga del individuo en la actuación final.
Alvero-Cruz et al. (2019) informó que la combinación del VO2 máx. y el porcentaje de grasa corporal explicaría el 83,9% del rendimiento durante un evento de 27 km y 1750 metros de desnivel positivo y negativo.
Por lo tanto, el VO2 máx. aparece como un parámetro esencial de rendimiento en trail running de corta distancia, sea cual sea el perfil de la carrera y la población estudiada. Finalmente, Lemire et al. (2020) han demostrado que la velocidad asociado con el VO2 máx. fue el principal predictor del rendimiento en una contrarreloj corriendo en ambas pendientes en un grupo homogéneo de corredores altamente entrenados.
El tercer factor de rendimiento descrito clásicamente en las carreras de resistencia es la EC (Daniels y Daniels, 1992; Foster y Lucia, 2007; Joyner y Coyle, 2008; McLaughlin et al., 2010). En el estudio de Ehrstrom (2018) no se observó correlación entre la EC medida en cinta con 0% o con pendiente del 10% y el rendimiento en carrera de TR de formato S. Sin embargo, esta falta de correlación concuerda con estudios previos que encontraron que no hay correlación entre la EC y el rendimiento en carreras de ruta entre los corredores de élite Kenianos (Mooses et al., 2015) o entre corredores europeos de sub-élite (Williams y Cavanagh, 1987). Asimismo, Balducci et al. (2017) no informaron correlación entre el desempeño en un evento de trail de categoría M (Km-esfuerzo: 75-114) y la EC medida en una cinta sin pendiente y cuesta arriba en un población heterogénea de corredores de pista. Sin embargo, se debe tener en cuenta que la EC10%, que requiere adoptando un patrón de zancadas más cercano al adoptado por los corredores en las porciones de ascensos del evento, permitió mejorar el R2 del modelo de rendimiento de senderos que han establecido.
Estos resultados sugieren la necesidad de una evaluación de la EC en un contexto más representativo del camino, es decir, terreno irregular, mediciones a diferentes velocidades y diferentes pendientes positivas y negativas.
De hecho, los corredores acostumbrados a correr por el suelo irregular, desarrollan una mejor EC en estos terrenos específicos (Jensen et al., 1999).
Esta información es útil para comprender el requisitos de la actividad, y dar indicaciones de las cualidades fisiológicas que deben evaluarse y dirigirse durante el entrenamiento con el fin de buscar un rendimiento más individualizado.
Autor
Prof. Lic. Guillermo Morea
AEIEF IdHICS CONICET UNLP
BE Trail Perf (evaluaciones morfo-funcionales)
Go Trail Run (capacitación – trail coaching)
3. Referencias
Abe, D., Fukuoka, Y., Muraki, S., Yasukouchi, A., Sakaguchi, Y., and Niihata, S. (2011). Effects of Load and Gradient on Energy Cost of Running. J. Physiol. Anthropol. 30, 153–160. doi:10.2114/jpa2.30.153.
Alvero-Cruz, J. R., Parent Mathias, V., Garcia Romero, J., Carrillo de Albornoz-Gil, M., Benítez-Porres, J., Ordoñez, F. J., et al. (2019). Prediction of Performance in a Short Trail Running Race: The Role of Body Composition. Front. Physiol. 10. doi:10.3389/fphys.2019.01306.
Balducci, P., Clemencon, M., Trama, R., and Hautier, C. A. (2017b). The calculation of the uphill energy cost of running from the level energy cost of running in a heterogeneous group of mountain ultra endurance runners. Asian J. Sports Med. doi:10.5812/asjsm.42091.
Barnes, K. R., and Kilding, A. E. (2014). Strategies to Improve Running Economy. Sport. Med. 45, 37–56. doi:10.1007/s40279-014-0246-y.
Berryman, Mujika, Arvisais, Roubeix, Binet, Bosquet, et al. (2016). Strength Training for Middle- and Long-Distance Performance: A Meta-Analysis. Int. J. Sports Physiol. Perform. 11, 86–95. doi:10.1123/ijspp.2015-0012.
Breiner, T. J., Ortiz, A. L. R., and Kram, R. (2018). Level, uphill and downhill running economy values are strongly inter-correlated. Eur. J. Appl. Physiol. 119, 257–264. doi: 10.1007/s00421-018-4021-x
Brueckner, J. C., Atchou, G., Capelli, C., Duvallet, A., Barrault, D., Jousselin, E., et al. (1991). The energy cost of running increases with the distance covered. Eur. J. Appl. Physiol. Occup. Physiol. 62, 385–389. doi:10.1007/BF00626607.
Buczek, F. L., and Cavanagh, P. R. (1990). Stance phase knee and ankle kinematics and kinetics during level and downhill running. Med. Sci. Sports Exerc. 22, 669–77. doi:10.1249/00005768-199010000-00019.
Bjorklund, G., Swaren, M., Born, D. P., & Stoggl, T. (2019). Biomechanical Adaptations and Performance Indicators in Short Trail Running. Frontiers in Physiology, 10, 506. doi:10.3389/fphys.2019.00506
Byrne, C., Eston, R. G., and Edwards, R. H. T. (2001). Characteristics of isometric and dynamic strength loss following eccentric exercise-induced muscle damage. Scand. J. Med. Sci. Sport. 11, 134–140. doi:10.1046/j.1524-4725.2001. 110302.x.
Cavagna, G. A., Heglund, N. C., Harry, J. D., and Mantovani, M. (1994). Storage and release of mechanical energy by contracting frog muscle fibres. J. Physiol. 481, 689–708. doi:10.1113/jphysiol.1994.sp020474.
Chen, T. C. C., Chen, H. L., Pearce, A. J., and Nosaka, K. (2012b). Attenuation of eccentric exercise-induced muscle damage by preconditioning exercises. Med. Sci. Sports Exerc. 44, 2090–2098. doi:10.1249/MSS.0b013e31825f69f3.
Curtin, N. A., & Davies, R. E. (1973). Chemical and mechanical changes during stretching of activated frog skeletal muscle. Cold Spring Harbor Symposia on Quantitative Biology, 37, 619-626. doi:10.1101/SQB.1973.037.01.074
Daniels, J., and Daniels, N. (1992). Running economy of elite male and elite female runners. Med. Sci. Sports Exerc. 24, 483–489. doi:10.1249/00005768-199204000-00015.
Dewolf AH, Penailillo LE, Willems PA. The rebound of the body during uphill and downhill running at different speeds. J Exp Biol. 2016;219(16):2276–88.
Dufour, S. P., Lampert, E., Doutreleau, S., Lonsdorfer-Wolf, E., Billat, V. L., Piquard, F., & Richard, R. (2004). Eccentric cycle exercise: training application of specific circulatory adjustments. Medicine & Science in Sports & Exercice, 36(11), 1900-1906. doi:10.1249/01.MSS.0000145441.80209.66
di Prampero, P. E. (2003). Factors limiting maximal performance in humans. European Journal of Applied Physiology, 90(3-4), 420-429. doi:10.1007/s00421-003-0926-z.
Ehrstrom, S., Tartaruga, M. P., Easthope, C. S., Brisswalter, J., Morin, J. B., & Vercruyssen, F. (2018). Short Trail Running Race: Beyond the Classic Model for Endurance Running Performance. Medicine & Science in Sports & Exercice, 50(3), 580-588. doi:10.1249/MSS.0000000000001467
Eston, R. G., Mickleborough, J., and Baltzopoulos, V. (1995). Eccentric activation and muscle damage : biomechanical and physiological considerations during downhill running. Br. J. Sports Med. 29, 89–94. doi:10.1136/bjsm.29.2.89.
Fletcher, J. R., and MacIntosh, B. R. (2017). Running Economy from a Muscle Energetics Perspective. Front. Physiol. 8. doi:10.3389/fphys.2017.00433.
Fornasiero, A., Savoldelli, A., Fruet, D., Boccia, G., Pellegrini, B., & Schena, F. (2018). Physiological intensity profile, exercise load and performance predictors of a 65-km mountain ultramarathon. Journal of Sports Sciences, 36(11), 1287-1295. doi:10.1080/02640414.2017.1374707
Foster, C., and Lucia, A. (2007). Running economy : the forgotten factor in elite performance. Sport. Med. 37, 316–319. doi:10.2165/00007256-200737040-00011.
García-Pinillos, F., Latorre-Román, P., Ramírez-Campillo, R., Párraga-Montilla, J. A., and Roche-Seruendo, L. E. (2019). How does the slope gradient affect spatiotemporal parameters during running? Influence of athletic level and vertical and leg stiffness. Gait Posture 68, 72–77. doi:10.1016/j.gaitpost.2018.11.008.
Giandolini M, Vernillo G, Samozino P, et al. Fatigue associated with prolonged graded running. Eur J Appl Physiol. 2016;116(10): 1859–73.
Gindre, C., and Lussiana, T. (2015). Ultra Trail : la premier en bas a gagné. Zatopek 35, 48–51.
Gottschall, J. S., and Kram, R. (2005a). Energy cost and muscular activity required for leg swing during walking. J. Appl. Physiol. 99, 23–30. doi:10.1152/japplphysiol.01190.2004.
Gottschall, J. S., and Kram, R. (2005b). Ground reaction forces during downhill and uphill running. J. Biomech. 38, 445–452. doi:10.1016/j.jbiomech.2004.04.023.
Jensen, K., Johansen, L., and Karkkainen, O.-P. (1999). Economy in track runners and orienteers during path and terrain running. J. Sports Sci. 17, 945–950. doi:10.1080/026404199365335.
Joyner, M. J., & Coyle, E. F. (2008). Endurance exercise performance: the physiology of champions. The Journal of Physiology, 586(1), 35-44. doi:10.1113/jphysiol.2007.143834
Jones, A. M. (1998). A five year physiological case study of an olympic runner. Br. J. Sports Med. 32, 39–43. doi: 10.1136/bjsm.32.1.39
Khassetarash, A., Hassannejad, R., Ettefagh, M. M., and Oskouei, A. E. (2019). Vibration settling time of the gastrocnemius remains constant during an exhaustive run in rear foot strike runners. J. Biomech. doi:10.1016/J.JBIOMECH.2019.06.026.
Lemire, M., Hureau, T. J., Favret, F., Geny, B., Kouassi, B. Y. L., Boukhari, M., et al. (2020). Physiological factors determining downhill vs uphill running endurance performance. J. Sci. Med. Sport. 221. doi:10.1016/j.jsams.2020.06.004.
Lima, L. C. R., and Denadai, B. S. (2015). Attenuation of eccentric exercise-induced muscle damage conferred by maximal isometric contractions: a mini review. Front. Physiol. 6, 300. doi:10.3389/fphys.2015.00300.
Liefeldt G, Noakes TD, Dennis SC. Oxygen delivery does not limit peak running speed during incremental downhill running to exhaustion. Eur J Appl Physiol Occup Physiol. 1992;64(6):493- 496
Lienhard, K., Lauermann, S. P., Schneider, D., Item-Glatthorn, J. F., Casartelli, N. C., & Maffiuletti, N. A. (2013). Validity and reliability of isometric, isokinetic and isoinertial modalities for the assessment of quadriceps muscle strength in patients with total knee arthroplasty. J Electromyogr Kinesiol, 23(6), 1283-1288. doi:10.1016/j.jelekin.2013.09.004
Margaria, R., Cerretelli, P., Aghemo, P., & Sassi, G. (1963). Energy cost of running. Journal of Applied Physiology, 18, 367-370. doi:10.1152/jappl.1963.18.2.367
McLaughlin, J. E., Howley, E. T., Bassett, D. R., Thompson, D. L., and Fitzhugh, E. C. (2010). Test of the classic model for predicting endurance running performance. Med. Sci. Sports Exerc. 42, 991–997. doi:10.1249/MSS.0b013e3181c0669d.
Midgley, A. W., Mc Naughton, L. R., and Wilkinson, M. (2006). The relationship between the lactate turnpoint and the time at VO2max during a constant velocity run to exhaustion. Int. J. Sports Med. 27, 278–282. doi: 10.1055/s-2005- 86566.
Minetti, A. E. (1995). Optimum gradient of mountain paths. J Appl Physiol (1985), 79(5), 1698-1703. doi:10.1152/jappl.1995.79.5.1698
Minetti, A. E., Moia, C., Roi, G. S., Susta, D., & Ferretti, G. (2002). Energy cost of walking and running at extreme uphill and downhill slopes. Journal of Applied Physiology, 93(3), 1039-1046. doi:10.1152/japplphysiol.01177.2001
Millet GY, Tomazin K, Verges S, et al. Neuromuscular consequences of an extreme mountain ultra-marathon. PLoS One. 2011; 6(2):e17059.
Montgomery, J. R., & Grabowski, A. M. (2018). The contributions of ankle, knee and hip joint work to individual leg work change during uphill and downhill walking over a range of speeds. Royal Society Open Science, 5(8), 180550. doi:10.1098/rsos.180550
Morgan, D. W., Martin, P. E., Krahenbuhl, G. S., & Baldini, F. D. (1991). Variability in running economy and mechanics among trained male runners. Medicine & Science in Sports & Exercice, 23(3), 378-383.
Mooses, M., Mooses, K., Haile, D. W., Durussel, J., Kaasik, P., and Pitsiladis, Y. P. (2015). Dissociation between running economy and running performance in elite Kenyan distance runners. J. Sports Sci. 33, 136–144. doi:10.1080/02640414.2014.926384
Noordhof, D. A., and Sandbakk, O. (2020). Performance-determining variables in long-distance events: should they be determined from a rested state or after prolonged submaximal exercise? Skeletal muscle in elite athletes: optimizing sprint and endurance performance View Project.
Pokora, I., Kempa, K., Chrapusta, S. J., & Langfort, J. (2014). Effects of downhill and uphill exercises of equivalent submaximal intensities on selected blood cytokine levels and blood creatine kinase activity. Biology of Sport, 31(3), 173-178. doi:10.5604/20831862.1111434.
Scheer V.., Basset P, Giovanelli N, Vernillo G, Millet GP, Costa RJS. Defining off-road running: a position statement from the Ultra Sports Science Foundation. Int J Sports Med. 2020;41:275-84.
Snyder KL, Kram R, Gottschall JS. The role of elastic energy storage and recovery in downhill and uphill running. J Exp Biol. 2012;215:2283–7.
Staab, J. S., Agnew, J. W., & Siconolfi, S. F. (1992). Metabolic and performance responses to uphill and downhill running in distance runners. Medicine & Science in Sports & Exercice, 24(1), 124-127
Townshend, A. D., Worringham, C. J., & Stewart, I. B. (2010). Spontaneous pacing during overground hill running. Medicine & Science in Sports & Exercice, 42(1), 160-169. doi:10.1249/MSS.0b013e3181af21e2
Toyomura, J., Mori, H., Tayashiki, K., Yamamoto, M., Kanehisa, H., & Maeo, S. (2018). Efficacy of downhill running training for improving muscular and aerobic performances. Applied Physiology, Nutrition, and Metabolism, 43(4), 403-410. doi:10.1139/apnm-2017-0538
Vernillo, G., Giandolini, M., Edwards, W. B., Morin, J. B., Samozino, P., Horvais, N., et al. (2016a). Biomechanics and Physiology of Uphill and Downhill Running. Sport. Med., 1–15. doi:10.1007/s40279-016-0605-y.
Williams, K. R., and Cavanagh, P. R. (1987). Relationship between distance running mechanics, running economy, and performance. J. Appl. Physiol. 63, 1236–45.