23 Abr Análisis y Utilización de Datos de Entrenamiento en el Ciclismo
Simon A. Jobson1, Louis Passfield 1, Greg Atkinson2, Gabor Barton2 y Philip Scarf 3
1Centre for Sports Studies, University of Kent, Chatham, Kent, Reino Unido.
2Research Institute for Sport and Exercise Science, Liverpool John Moores University, Liverpool, Reino Unido.
3Centre for OR and Applied Statistics, University of Salford, Salford, Reino Unido.
RESUMEN
La mayoría de los modelos matemáticos de entrenamiento deportivo requieren la cuantificación de la intensidad y la cantidad o “dosis” de entrenamiento. Nuestro objetivo consistió en reunir los métodos disponibles para dicha cuantificación, particularmente en relación con el ciclismo, y las técnicas matemáticas que pueden ser utilizadas para plantear modelos sobre la relación entre el entrenamiento y el rendimiento. Los atletas de resistencia han utilizado el volumen de entrenamiento (kilómetros por semana y/o horas por semana) como índice de dosis de entrenamiento con cierto éxito. Sin embargo, estos métodos no suelen adaptarse a la influencia potencialmente importante de la intensidad del entrenamiento. La literatura científica ha proporcionado cierto apoyo a métodos alternativos como el índice de esfuerzo percibido de la sesión, que aporta una cuantificación subjetiva de la intensidad del ejercicio; y el método del impulso de entrenamiento derivado de la frecuencia cardíaca (TRIMP), que cuantifica el estímulo de entrenamiento como un compuesto de la carga externa y la respuesta fisiológica, multiplicando la carga de entrenamiento (estrés) por la intensidad del entrenamiento (esfuerzo). Otros métodos descriptos en la literatura científica son ‘la categorización ordinal’ y un método de exceso de consumo de oxígeno post-ejercicio basado en la frecuencia cardíaca. En ciclismo, los potenciómetros (por ejemplo, SRM ™ y PowerTap ™) se encuentran ampliamente disponibles. Estos dispositivos permiten la medición continua del ritmo de trabajo de los ciclistas (producción de potencia) cuando pedalean en sus propias bicicletas durante el entrenamiento y las competencias. Sin embargo, la variabilidad inherente en la producción de potencia al pedalear plantea varios desafíos cuando se desea evaluar la naturaleza exacta de una sesión. Tal variabilidad significa que la producción de potencia promedio es desproporcionada con respecto al esfuerzo fisiológico del ciclista. Una alternativa útil puede ser el uso de un proceso de promedio ponderado exponencialmente para representar los datos en forma de ‘potencia normalizada’. Varios grupos de investigación han aplicado la teoría de sistemas para analizar las respuestas al entrenamiento físico. Los modelos de impulso-respuesta tienen como objetivo relacionar las cargas de entrenamiento con el rendimiento, teniendo en cuenta las características dinámicas y temporales del entrenamiento y, por tanto, los efectos de las secuencias de carga a lo largo del tiempo. A pesar de los éxitos de este enfoque, tiene algunas limitaciones importantes, por ejemplo, se necesita una gran cantidad de pruebas de rendimiento para determinar los parámetros del modelo. Las redes neuronales artificiales no lineales pueden proporcionar una descripción más precisa del complejo proceso de adaptación biológica no lineal. Sin embargo, estos modelos también pueden estar restringidos por la gran cantidad de conjuntos de datos necesarios para “entrenar” el modelo. Algunos de los métodos matemáticos alternativos tales como el Performance-Potencial-Metamodel (PerPot), el modelo lineal mixto, los análisis de agrupamientos y la teoría del caos tienen una gran riqueza conceptual. Sin embargo, se requiere mucha más investigación antes de que estos enfoques puedan ser considerados como alternativas viables a los modelos tradicionales de impulso-respuesta. Es posible que algunos de estos métodos no aporten información útil sobre la relación entre el entrenamiento y el rendimiento. Sin embargo, pueden ayudar a describir el complejo fenómeno de respuesta al entrenamiento fisiológico.
INTRODUCCIÓN
Los científicos que han estudiado el entrenamiento físico han identificado diferentes funciones para el volumen, la intensidad y la frecuencia del entrenamiento en el proceso de adaptación [1]. Con el fin de optimizar el rendimiento cuando se trabaja con atletas de élite, es esencial que el entrenador deportivo tenga sólidos conocimientos sobre la relación entre entrenamiento y rendimiento. Se ha demostrado que esta relación es altamente individual debido a la variación en factores tales como los antecedentes de entrenamiento individual [2], la genética [3] y factores psicológicos [4]. Para profundizar estos conocimientos, se han desarrollado varios modelos matemáticos con el fin de describir el aspecto dinámico del entrenamiento y las consecuencias de las cargas de entrenamiento sucesivas a lo largo del tiempo [4-6].
CUANTIFICACIÓN DEL ENTRENAMIENTO
La mayoría de los modelos matemáticos de entrenamiento deportivo demandan la cuantificación de la intensidad y la cantidad o “dosis” del entrenamiento. Idealmente, esta cuantificación requiere que los investigadores incorporen parámetros para la intensidad, la duración y la frecuencia. Los atletas de resistencia han utilizado con cierto éxito el volumen de entrenamiento (kilómetros por semana y/o horas por semana) como un índice de dosis de entrenamiento [7,8]. Sin embargo, este índice no tiene en cuenta la potencialmente importante influencia de la intensidad del entrenamiento. Por lo tanto, se han investigado otros métodos alternativos.
Índice de Esfuerzo Percibido de la Sesión
El índice de esfuerzo percibido (RPE) proporciona un método para cuantificar subjetivamente la intensidad del ejercicio [9]. Definido por la intensidad de la incomodidad o fatiga percibida en un momento particular, se ha demostrado que el RPE se correlaciona con la intensidad del esfuerzo [10]. Para proporcionar un índice de una sesión de entrenamiento completa, Foster et al. [11] desarrollaron la escala de RPE de la sesión (sRPE) como una modificación de la escala estándar del RPE. En lugar de proporcionar una puntuación de RPE para un aspecto específico (por ejemplo, intervalo/serie) de una sesión de ejercicio, el sRPE tiene como objetivo proporcionar un RPE para la sesión como un todo, es decir, integrar la totalidad de las señales de intensidad -ejercicio [10]. Se ha demostrado que la escala de sRPE es un método confiable y válido para cuantificar la intensidad durante ejercicios aeróbicos y ejercicios de resistencia cuando se compara con las mediciones basadas en frecuencia cardíaca [10,12,13].
Categorización Ordinal
El entrenamiento también se ha categorizado en niveles ordinales en función de las diferencias de intensidad. Aunque esta clasificación ha sido arbitraria en algunos casos, [14] habitualmente este enfoque se basa en la relación entre una variable medida, tal como la velocidad y la frecuencia cardíaca [15] o la respuesta del lactato [2]. A cada categoría se le asigna un coeficiente de ponderación arbitrario que enfatiza las sesiones de entrenamiento de alta intensidad. Al estar basada en las respuestas fisiológicas de un individuo y asumiendo que no existe una respuesta no lineal frente a la creciente intensidad del ejercicio, estos métodos parecen más defendibles científicamente. Sin embargo, queda un elemento de subjetividad debido a la ponderación arbitraria de las categorías de intensidad. Además, el uso de la frecuencia cardíaca en el proceso de cuantificación del entrenamiento tiene una serie de limitaciones. Independientemente de la intensidad del ejercicio, el ritmo cardíaco puede variar debido a factores tales como la deriva cardíaca [16], los cambios en la temperatura [17] el estado de hidratación y la posición del cuerpo en la bicicleta [16].
Recuperación de Frecuencia Cardíaca e Impulso de Entrenamiento
Para superar algunas de las limitaciones anteriores, Borresen y Lambert [18,19] sugirieron que, como marcadores indirectos de la función autonómica, la variabilidad de la frecuencia cardíaca y, en particular, la recuperación de la frecuencia cardíaca, pueden ser consideradas formas prácticas para la cuantificación de los efectos fisiológicos del entrenamiento. Sin embargo, se necesitan muchos más trabajos para demostrar que estos métodos tienen una aplicación práctica en la prescripción de programas de entrenamiento óptimos [19].
El impulso de entrenamiento (TRIMP) cuantifica el estímulo de entrenamiento como un conjunto formado por la carga y la respuesta fisiológica, multiplicando la carga de entrenamiento (estrés) por la intensidad del entrenamiento (tensión) [20]. La fórmula original de Banister y Calvert [21] fue modificada por Morton et al. [22] para incluir un factor multiplicativo que diera mayor peso al entrenamiento de alta intensidad (ecuación 1):
Ecuación 1: TRIMP= duración del ejercicio x fracción de la reserva de frecuencia cardíaca x e (fracción de la reserva de frecuencia cardíaca b)
Donde e es el número de Euler, 2,718, y b es una constante basada en la respuesta del lactato en sangre durante el ejercicio incremental y es igual a 1,92 en varones y 1,67 en mujeres.
Existen ventajas en el uso del método TRIMP, que se evidencian no solo por la cantidad de investigadores que han explorado el uso de esta métrica [23-25]. El TRIMP es relativamente fácil calcular con un monitor de frecuencia cardíaca económico y de uso común. Este enfoque arroja un número único que representa el estímulo de entrenamiento proporcionado por toda la sesión. Sin embargo, la formulación original de Banister del concepto TRIMP no tenía en cuenta los efectos específicos del sistema energético de la intensidad del entrenamiento. Si bien, hasta cierto punto, el factor de ponderación de Morton supera esta deficiencia, todavía es limitado porque asume una relación fija entre la frecuencia cardíaca y las respuestas de lactato; un supuesto que Hurley et al. [26] cuestionan.
Exceso de Consumo de Oxígeno después del Ejercicio
Los métodos sRPE y TRIMP han recibido apoyo en la literatura científica, pero ninguno de los dos métodos cuenta con el sustento de una teoría fisiológica. Para cuantificar la alteración homeostática asociada con el entrenamiento se pueden determinar las variables fisiológicas tradicionales tales como el consumo de oxígeno, la frecuencia cardíaca y el lactato sanguíneo. Sin embargo, estas últimas medidas solo reflejan una respuesta momentánea al ejercicio. La concentración de lactato en sangre, medida durante o después del ejercicio, también puede depender del sitio de muestreo. Por el contrario, se ha sugerido que la medición del exceso de consumo de oxígeno tras el ejercicio (EPOC) refleja la respuesta acumulada del cuerpo frente a una sesión de entrenamiento completa. Al igual que con la medición del consumo de oxígeno y de la respuesta del lactato, la evaluación de EPOC debe ser realizada en un laboratorio, es costosa, requiere mucho tiempo y, por lo tanto, no es apropiada para una evaluación regular. Reconociendo esta limitación, Rusko et al. [27] desarrollaron un modelo de predicción de EPOC (EPOC basado en HR) basado en la frecuencia cardíaca, que se describe matemáticamente como la ecuación 2:
EPOC(t)= f(EPOC(t-1),% VO2maxΔt) (Ecuación 2)
EPOC en el tiempo t (EPOC (t)) se estima utilizando las variables de la intensidad actual (% VO2max), la duración del ejercicio (tiempo entre dos puntos de muestreo [Δt]) y EPOC en el punto de muestreo anterior (EPOC (t – 1)). Este modelo fue validado en un grupo de 32 sujetos adultos sanos, el EPOC basado en HR arrojó una buena correlación con el EPOC medido (r = 0,89) [27]. Los valores de error absoluto medio de EPOC basado en HR, cuando se compara con los valores de EPOC medidos, fueron 9,4, 14,0 y 16,9 m L/kg para ejercicios con una carga constante de 40% y 70% y ejercicio incremental máximo, respectivamente. Sin embargo, a pesar de lo atractivo que puede parecer este modelo, el cálculo es relativamente complejo y actualmente requiere software y hardware patentados (por ejemplo, monitor de frecuencia cardíaca Suunto ™ t6). Además, el modelo se validó en un solo estudio, en el que solo se investigó el ejercicio de corta duración (2×10 min) [27].
Producción de Potencia
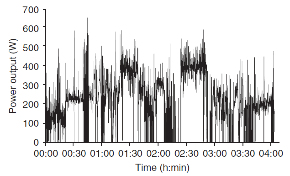
Las potenciómetros (por ejemplo, SRM ™ y PowerTap™) son en la actualidad muy accesibles y permiten la medición continua de la tasa de trabajo de los ciclistas (producción de potencia) cuando pedalean en sus propias bicicletas durante el entrenamiento y las competencias. De hecho, en un estudio realizado con estos dispositivos, los autores concluyeron que “las mediciones con un error tan bajo podrían ser adecuadas para hacer un seguimiento de los pequeños cambios en el rendimiento competitivo que son fundamentales para los ciclistas de élite “[28]. En consecuencia, estos dispositivos han sido ampliamente utilizados por ciclistas de élite durante el entrenamiento y las competencias. Por lo tanto, con estas bicicletas instrumentadas ahora es posible examinar en detalle el rendimiento del entrenamiento realizado y el rendimiento en las competencias y las respuestas fisiológicas asociadas. En la Figura 1 se presenta un ejemplo de cómo se observan los datos típicos recopilados durante una sesión de entrenamiento. Esta capacidad para cuantificar con precisión el trabajo mecánico del entrenamiento, así como el detalle y la magnitud de estos datos, hace que el ciclismo sea único porque permite conocer las exigencias de la preparación y de la competencia deportiva. Sin embargo, también se puede ver que la variabilidad inherente en la producción de potencia durante el entrenamiento plantea varios desafíos cuando se desea evaluar la naturaleza exacta de cualquier sesión de entrenamiento.
Figura 1. Ejemplo de datos de producción de potencia de entrenamiento medidos con un sistema SRM ™ para las palancas de la bicicleta.
Como resultado de las dificultades en la interpretación de los datos de producción de potencia, lo que realizan en la práctica muchos atletas y entrenadores es simplemente inspeccionar visualmente las sesiones de entrenamiento individuales (por ejemplo, como se presenta en la Figura 1). De esta forma, se pueden identificar características generales de la sesión, como el punto en el que se alcanzó la producción de potencia más alta, la cantidad de intervalos completados o el nivel de variación de la producción de potencia. Claramente, tales métodos no permiten un análisis completo de los datos disponibles. Un enfoque alternativo consiste en evaluar la cantidad de tiempo que se pasa dentro de determinadas “franjas” o “zonas” de potencia mediante un histograma. Ebert et al.[29] proporcionaron una comparación gráfica de dos tipos de carreras de ciclismo de ruta de la Copa del Mundo femenina evaluando el porcentaje del tiempo total de carrera transcurrido en cuatro grupos de potencia (0–100 W, 100–300 W, 300– 500 W y > 500 W). Reconociendo la importante influencia de la masa corporal en el rendimiento en ciclismo, Ebert et al. [30] proporcionaron comparaciones similares de producción de potencia por unidad de masa corporal (W/kg) en un grupo de ciclistas varones profesionales de carreras por etapas. Aunque simple, este método es excelente para las comparaciones de sesiones completas [31]. Sin embargo, el enfoque del histograma está limitado por su incapacidad para reconocer esfuerzos separados dentro de una determinada zona de potencia.
Por ejemplo, este método no puede diferenciar entre un esfuerzo único de 5 minutos a 350 W y cinco intervalos de 1 minuto con la misma intensidad, aunque el efecto de estos dos ejercicios sobre los parámetros asociados al entrenamiento puede ser muy diferente [32].
Potencia Promedio
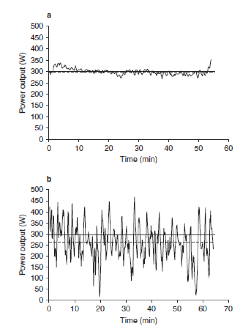
La producción de potencia nos aporta una medida directa e inmediata de la tasa de trabajo, en oposición a la respuesta perceptiva o cardiovascular del atleta frente a esa intensidad de ejercicio. Sin embargo, como se discutió en la sección 1.5, la naturaleza estocástica de la tasa de trabajo cuando se realiza ciclismo al aire libre [33] hace que la interpretación de la información de los potenciómetros que se colocan en la bicicleta sea problemática. Un enfoque simple es calcular la potencia media o promedio durante la duración del entrenamiento. Sin embargo, la potencia media no necesariamente coincide con la tensión fisiológica del ciclista a menos que la sesión de entrenamiento sea de potencia constante por naturaleza. Por ejemplo, un esfuerzo máximo en una prueba contrarreloj de 1 hora sobre terreno plano puede dar lugar a una potencia media de 299 W y requiere variación en la producción de potencia a lo largo de la carrera (Figura 2a). En contraste, un esfuerzo máximo con marcados cambios de ritmo, por ejemplo, en una carrera tipo criterium o una contrarreloj montañosa, puede hacer que el ciclista produzca una producción de potencia promedio mucho mas baja de sólo 260 W (Figura 2b). Las investigaciones futuras deberían tratar de describir en detalle cuáles diferencias en la potencia general son para ciclismo de potencia variable versus potencia constante.
Figura 2. Media móvil de 30 segundos de potencia para una contrarreloj en el llano (a) y un criterium (b) realizadas por el mismo ciclista. Es necesario tener en cuenta que la potencia promedio (línea discontinua) varía ampliamente entre los esfuerzos, mientras que la potencia normalizada (línea continua) es similar, lo que indicaría un costo fisiológico equivalente para ambos esfuerzos.
Reconociendo las limitaciones del enfoque de potencia media, Coggan [34] propuso el uso de un proceso de promedio ponderado exponencialmente para representar los datos. Los datos se suavizan usando una media móvil de 30 segundos (porque muchos procesos fisiológicos [por ejemplo, VO2, frecuencia cardíaca] responden a cambios en la intensidad del ejercicio con una constante de tiempo de ~ 30 s) antes de ser elevados a la cuarta potencia (derivada de una regresión de la concentración de lactato en sangre frente a la intensidad del ejercicio). Finalmente, los valores transformados se promedian y se obtiene la raíz cuarta lo que arroja una ‘potencia normalizada‘. Usando este proceso, teóricamente es posible hacer comparaciones más directas entre diferentes tipos de sesiones de entrenamiento. En el ejemplo anterior, por ejemplo, el esfuerzo contrarreloj normalizado sigue siendo de unos 299 W (figura 2a), pero el esfuerzo variable de 260 W normalizado se convierte en 291 W (figura 2b). Si bien este método ha captado considerable interés en la comunidad del ciclismo, hasta ahora ha recibido muy poca evaluación crítica de la comunidad científica [35].
Análisis del Espectro de Potencia
La capacidad de avanzar al pedalear requiere energía para superar la resistencia ambiental (principalmente la resistencia al viento, al rodamiento y gravitacional [36]). Por lo tanto, la variación de estas fuerzas resistivas al pedalear da como resultado cambios predecibles en la producción de potencia. Sin embargo, más allá de estas relaciones físicas, Hu et al. [37] sugirieron que “otras” fluctuaciones en los datos de los sistemas biológicos plantean un “ruido”, que es el resultado de procesos aleatorios o de estímulos externos que inciden sobre el sistema. Si este ruido fuera el resultado de factores aleatorios, un análisis del espectro de potencia revelaría una señal de ruido blanco gaussiano (es decir, donde todas las frecuencias tienen la misma ponderación de potencia) [38]. Tucker y col [39]. utilizaron una transformación discreta de Fourier (DFT) para evaluar el espectro de potencia de la producción de potencia de ciclistas aficionados. Una DFT expresa los datos como una suma de formas de onda sinusoidales de frecuencia variable (Figura 3), y el espectro de la señal es la señal que describe la forma en que las amplitudes y fases de estas formas de onda cambian con la frecuencia. Por lo tanto, en una frecuencia específica es posible obtener la medida de la contribución que una forma de onda específica provocará en la señal. Con este método, Tucker et al. [39] demostraron la presencia de picos de frecuencia dominantes (en eventos de ciclismo de distancias de ~ 2.5, ~ 6, ~ 12 y ~ 21 km) durante una prueba contrarreloj de 20 km en laboratorio, lo que sugiere que las fluctuaciones de producción de potencia observadas no fueron de hecho aleatorias. Tucker y col. [39] propusieron que las fluctuaciones en la producción de potencia eran el resultado de la regulación de la producción de potencia producida por procesos biológicos de control intrínseco. También se observaron diferentes picos de frecuencias dominantes al analizar el espectro de frecuencias de los componentes individuales de la contrarreloj (es decir, comienzo, medio y final) y de la prueba contrarreloj completa. Se sugirió que cada uno de estos picos dominantes representaban un sistema de control diferente o un componente de un sistema general. Sería muy interesante investigar si tales efectos se repiten en un mayor conjunto de datos y durante períodos mas largos (por ejemplo, días, meses) que los considerados por estos autores.
Tucker y col. [39] también investigaron el nivel de auto-semejanza en la señal de producción de potencia de pruebas contrarreloj de los ciclistas utilizando un análisis fractal. En este contexto, el concepto de auto-semejanza se refiere a la propiedad de que las partes de la señal fractal son similares al todo. A pesar de la gran variabilidad en la producción de potencia generada tanto dentro como entre las pruebas, estos autores observaron que la dimensión fractal del espectro de potencia era similar (1,56–1,9) en todos los sujetos. Por lo tanto, a pesar de la señal irregular del espectro de potencia, parecería haber un grado de auto-semejanza entre las partes de la señal y la señal como un todo. Tucker y col. [39] sugirieron que esta concordancia en la señal indica un proceso de control general similar presente en cada ciclista y durante cada contrarreloj. Las investigaciones adicionales deberían intentar establecer si tales hallazgos reflejan fenómenos fisiológicos reales o, si por el contrario, simplemente reflejan la amplia aplicabilidad de los fractales.
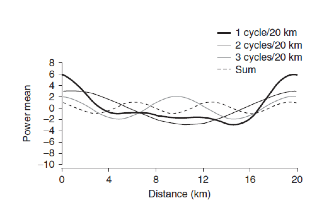
Figura 3. Ejemplo de una transformación de Fourier que expresa los datos como una suma de ondas sinusoidales de frecuencia variable. En este ejemplo, se sumaron tres tipos de onda sinusoidales para crear una señal de potencia que se asemejara a los datos de producción de potencia observados durante una prueba contrarreloj de 20 km (reproducido de Tucker et al., [39] con autorización).
PLANTEO DE MODELOS DE LA RELACIÓN ENTRE ENTRENAMIENTO Y RENDIMIENTO
Los modelos pueden ser puramente empíricos o pueden estar basados en una apreciación detallada de la estructura subyacente [20]. Claramente, estas estructuras subyacentes pueden ser extremadamente complejas. Aunque los modelos matemáticos se basan en abstracciones del sistema real, persiste el interrogante de cuánta estructura subyacente es necesario incorporar en los modelos de entrenamiento y rendimiento.
Modelos de Impulso-Respuesta
Sobre la base de las primeras investigaciones de Banister et al. [4] varios grupos de investigación han aplicado la teoría de sistemas para analizar las respuestas al entrenamiento físico [2,40,41]. Este enfoque intenta resumir un proceso dinámico en un modelo matemático, y el sistema estaría caracterizado por al menos una entrada (imput) y una salida (output) relacionadas mediante una “función de transferencia” matemática [42]. Esta función tiene la forma general (ecuación 3):
Rendimiento del modelo= (fitness/aptitud física del modelo de entrenamiento)- K (fatiga del modelo de entrenamiento) (Ecuación 3)
donde K es una constante que se ajusta en función de la magnitud del efecto de fatiga en relación con el efecto de aptitud. [20]. Calvert y col. [14] presentaron un modelo simple en el que un solo impulso de entrenamiento provocaba dos respuestas de aptitud que aumentarían el rendimiento y una respuesta de fatiga que disminuiría el rendimiento. Así, los modelos de ‘impulso-respuesta’ tienen como objetivo relacionar las cargas de entrenamiento con el rendimiento, teniendo en cuenta las características dinámicas y temporales del entrenamiento y, por tanto, los efectos de las secuencias de carga a lo largo del tiempo.
Este modelo se ha presentado en diferentes formas matemáticas, y las mas notables son las ecuaciones diferenciales de Calvert et al. [14], Morton et al. [22], Busso et al. [43], Fitz- Clarke y otros [44] y Busso et al. [45] que se han basado en estas formulaciones para presentar curvas de influencia que brindan una imagen clara de cómo una sesión de entrenamiento específica afecta el rendimiento en el futuro. De hecho, Busso et al. [45] observaron que las ‘ influencias’ positivas y negativas (PI y NI) estaban en realidad más cerca de las variaciones en el rendimiento que los valores calculados por las funciones positivas y negativas (PF y NF) producidas en el modelo matemático subyacente en sí (i.e, donde PF y NF representan una ganancia de aptitud inmediata y PI y NI representan una ganancia de aptitud atrasada biológicamente más plausible).
Se ha utilizado una variedad de tipos de datos como entradas en los modelos de tipo de respuesta a impulso. Para predecir el rendimiento de dos corredores que no eran de élite, Morton et al. [22] cuantificaron el impulso de entrenamiento utilizando TRIMP. En uno de los sujetos, la concordancia entre el rendimiento medido y el estimado fue excelente (R2 = 0,96), mientras que en el segundo fue menos impresionante (R2 = 0,71). Mediante la utilización de la categorización ordinal del entrenamiento, Mujika et al. [2] identificaron relaciones más débiles, y la variación explicada en el rendimiento iba desde R2 = 0,45 a R2 = 0,85 en un grupo de nadadores de élite. Una explicación propuesta para esta variabilidad es que los parámetros del modelo cambian con el tiempo (es decir, entrenamiento). Por lo tanto, Busso et al. [46] compararon tanto un modelo variable en el tiempo como un modelo que no variaba en el tiempo, con R2= 0.88 y R2=0,68 respectivamente. Sin embargo, el uso del modelo y sus parámetros para predecir las respuestas al entrenamiento futuro se descarta en el enfoque que varía en el tiempo, a menos que los parámetros cambien de una manera predecible [20].
El modelo de impulso-respuesta proporciona información pertinente sobre las diferencias interindividuales y permite la construcción de programas de entrenamiento individualizados [47]. Sin embargo, tanto el modelo Banister original como sus extensiones tienen algunas limitaciones importantes. Taha y Thomas [20] argumentaron que el modelo no concuerda con los conocimientos contemporáneos de los mecanismos fisiológicos, requiere un número excesivo de pruebas de rendimiento para determinar los parámetros del modelo y es incapaz de distinguir los efectos específicos de diferentes impulsos de entrenamiento. Además, la variabilidad entre estudios y entre sujetos en las estimaciones de los parámetros limita la capacidad de aplicar una versión genérica del modelo.
Redes Neuronales
Los modelos tradicionales de impulso-respuesta como los descriptos en la sección 2.1 se basan en conceptos matemáticos lineales como el análisis de regresión y las ecuaciones diferenciales lineales. Sin embargo, debido a que la adaptación de un sistema biológico produce cambios en el propio sistema, la adaptación biológica es realmente un problema complejo no lineal [48]. Por esta razón, Edelmann-Nusser et al. [48] utilizaron una red neuronal de perceptrón multicapa no lineal para modelar el rendimiento de un nadador de nivel olímpico. Este modelo produjo un ‘error de predicción’ de solo 0,04%.
Un problema asociado con las redes neuronales es que normalmente requieren muchos conjuntos de datos para “entrenar” al modelo. Teniendo diez neuronas de entrada, dos neuronas ocultas y una neurona de salida, el entrenamiento del modelo utilizado por Edelmann-Nusser et al. [48] requirió 40 conjuntos de datos (este número se incrementa a 60 con la adición de una sola neurona en la capa oculta). Por lo tanto, transcurrirá cierto tiempo antes de que dicho modelo sea útil para cualquier atleta dado. Edelmann-Nusser y col. [48] superaron este problema entrenando el modelo con los conjuntos de datos de otro atleta. En última instancia, este método resultó ser un éxito, pero, como señalaron los autores, podría haber sido fortuito que el comportamiento adaptativo de ambos atletas fuera similar. Aunque el poder predictivo es impresionante, Hellard et al. [47] han advertido que la mayor debilidad de los modelos de redes neuronales es que no identifican explícitamente las relaciones causales, es decir, funcionan como una “caja negra”.
Metamodelo Dinámico
El Performance-Potential-Metamodel (Per-Pot) descrito por Perl [6] simula la interacción entre la carga y la interacción del rendimiento mediante dinámicas antagónicas. Hellard et al. [47] destacaron la riqueza conceptual de este modelo en el sentido de que explica el efecto colapso provocado por la sobrecarga de entrenamiento, la atrofia asociada con el desentrenamiento y el comportamiento a largo plazo de la relación entrenamiento-rendimiento.
Similar al modelo Banister, el concepto básico del modelo PerPot es el de antagonismo (Figura 4). Cada impulso de carga alimenta un potencial de tensión y un potencial de respuesta. A su vez, estos potenciales de amortiguación influyen en el potencial de rendimiento, donde el potencial de respuesta aumenta el potencial de rendimiento (retrasado por el retraso en el flujo de respuesta) y el potencial de tensión reduce el potencial de rendimiento (retrasado por el retraso en el flujo de tensión). Si se sobrecarga el potencial de tensión, se produce un desborde que tiene un impacto negativo adicional en el potencial de rendimiento. Si bien este modelo es atractivo, según el conocimiento de los autores, hasta el momento ningún investigador ha aportado una validación crítica.
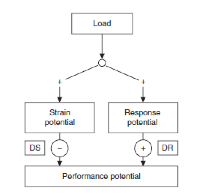
Figura 4. Estructura antagonista del modelo de Performance-Potencial-Metamodel. DR= Retraso en el flujo de respuesta; DS= Retraso en el flujo de tensión; Load= Carga; Strain potential= Potencial de Tensión; Response Potential= Potencial de respuesta; Performance potential= Potencial de rendimiento.
Modelo de Regresión Múltiple y Lineal Mixto
Como se describió anteriormente (sección 2.1), uno de los problemas asociados con el modelo Banister es la necesidad de contar con una gran cantidad de puntos de datos por parámetro. Para asegurar una solución estable en un análisis de regresión, Stevens [49] recomendó un mínimo de 15 observaciones por variable predictiva. Para evitar estas dificultades, se ha sugerido el modelo de regresión múltiple como una alternativa viable, especialmente cuando hay relativamente pocas mediciones repetidas disponibles para diferentes sujetos [47]. Este método permite la integración de cargas de entrenamiento como variables independientes y puede tener en cuenta los efectos de las secuencias de carga a lo largo del tiempo. Mujika et al. [50] utilizaron una regresión escalonada para crear un modelo para la relación entre entrenamiento y rendimiento y obtuvieron un nivel de concordancia muy cercano al del modelo Banister.
Los modelos lineales mixtos pueden ser aplicados a datos de medidas repetidas de diseños no balanceados (por ej, múltiples variables independientes con múltiples niveles no balanceados en cada factor). A diferencia del modelo Banister, que genera un modelo personal para cada sujeto, los modelos mixtos se adaptan a la heterogeneidad de los sujetos y permiten que los parámetros varíen entre los individuos a medida que se construye un modelo de comportamiento poblacional [5]. Por lo tanto, este tipo de análisis también puede hacer frente a la combinación de efectos aleatorios y fijos que se producen con los datos del “mundo real” [51]. Por ejemplo, los datos relacionados con el rendimiento pueden verse influidos por fluctuaciones aleatorias en factores ambientales, así como por cambios sistemáticos en el entrenamiento que introduce el entrenador. En general, todos los datos se utilizan para construir la parte del modelo que será común a la población completa de sujetos, aunque solo las observaciones específicas de cada individuo se utilizan para construir la parte personal del modelo. Por lo tanto, la influencia relativa de cada parte del modelo dependerá, de los datos disponibles, y habrá una contribución más fuerte proveniente de los datos de la población cuando los datos individuales sean deficientes y viceversa [5]. Los modelos lineales mixtos también pueden hacer frente a datos faltantes y modelos ‘anidados’ (jerárquicos). Un modelo jerárquico podría ser relevante para la investigación del mundo real cuando, por ejemplo, los sujetos no pueden considerarse mutuamente excluyentes, por ejemplo, los atletas que entrenan entre sí como parte de un equipo.
Los modelos lineales mixtos se han utilizado para analizar datos en psicología, [52] datos obtenidos con biochips (microarray) [53] y datos agrícolas [54]. Sin embargo, este tipo de análisis ha sido poco utilizado en las ciencias del deporte y del ejercicio. De hecho, en aquellos campos en que fue utilizado, no parece haber tenido una gran capacidad de predicción. Avalos y col. [5] descubrieron que los modelos mixtos describían la relación entre el entrenamiento y el rendimiento, pero que el coeficiente de determinación promedio era de solo 0,38. No quedan dudas de que es necesario seguir trabajando para determinar la factibilidad de la aplicación de los modelos mixtos en un contexto deportivo. Un tema importante, que necesita una consideración cuidadosa, es cómo se identifica y aplica la estructura de covarianza de medidas repetidas mas adecuada en el modelado lineal mixto.
Análisis de Agrupamiento
El análisis de agrupamiento se ha utilizado en una amplia gama de contextos deportivos, desde la detección del consumo de sustancias prohibidas [55] hasta el análisis de la transferencia de peso durante un swing de golf [56]. De hecho, el análisis de agrupamientos puede proporcionar una herramienta útil para identificar las respuestas del grupo al entrenamiento. Avalos y col. [5] investigaron la relación entre los períodos de entrenamiento a corto, mediano y largo plazo y el rendimiento utilizando análisis de componentes principales y análisis de agrupamiento. Se identificaron dos factores de componentes principales con el análisis de agrupamientos que aportan una confirmación estadística de las cuatro diferentes respuestas al entrenamiento basadas en estos dos componentes. Los cuatro agrupamientos de entrenamiento identificaron una respuesta variable (es decir, una combinación de reacciones positivas, negativas o neutrales) frente a cada uno de los tres períodos de entrenamiento independientemente de las diferencias en la carga de entrenamiento entre los sujetos.
Dinámica No Lineal y Teoría del Caos
La teoría del caos es un conjunto de métodos que estudian los fenómenos no lineales. Específicamente, el caos es un fenómeno que parece localmente impredecible, pero, de hecho, es globalmente estable, presenta límites claros y muestra una gran sensibilidad a las condiciones iniciales. Un excelente ejemplo de caos en el cuerpo humano son los latidos del corazón [57]. El ritmo cardíaco normal parece periódico. Sin embargo, instrumentos sensibles han revelado que el ritmo cardíaco normal muestra una pequeña variabilidad en el intervalo entre latidos [58]. Esta variación de la señal es el resultado de la interacción entre los sistemas nerviosos simpático y parasimpático, lo que finalmente crea una diversidad de señales significativas y un ritmo cardíaco complejo e impredecible [59]. La ventaja de esta falta de periodicidad es que el sistema está mejor equipado para adaptarse a las demandas cambiantes. El corazón también muestra dos características adicionales de los sistemas caóticos: el surgimiento del orden [60] y la existencia de atractores extraños [61].
Si bien la teoría del caos ha sido aplicada a diversos fenómenos biológicos, [62,63] para los autores, este enfoque aún no ha sido considerado en el contexto de la teoría del entrenamiento. A partir de las discusiones anteriores, queda claro que la relación entre los múltiples factores involucrados en el desarrollo del entrenamiento es un problema dinámico no lineal. Sin embargo, también es probable que las interacciones constantemente cambiantes entre estos factores originen un sistema oscilante predominantemente estable. El uso de la teoría del caos para identificar los atractores clave (y la relación entre estos atractores) en este sistema podría ampliar aún mas nuestra comprensión de las respuestas al entrenamiento tanto individuales como grupales. Además, la teoría del caos podría describir la pérdida del control del sistema asociada con el sobreentrenamiento, un escenario análogo a los extensos estudios de fibrilación auricular llevados a cabo utilizando la teoría del caos [64, 65].
CONCLUSIONES
En esta revisión, hemos discutido los métodos disponibles para cuantificar el impulso de entrenamiento en ciclismo y los métodos disponibles para modelar la relación entre este impulso de entrenamiento y el rendimiento. Muchos de los métodos discutidos son aplicables a una amplia gama de deportes; sin embargo, el ciclismo es uno de los pocos deportes que pueden aprovechar la gran cantidad de datos proporcionados por la medición continua de la tasa de trabajo (producción de potencia).
Las series individuales de entrenamiento/competencia pueden ser cuantificadas utilizando métodos como sRPE, TRIMP y EPOC basada en la frecuencia cardíaca (HR). La medición de la producción de potencia permite cuantificar las sesiones por medio de diferentes metodologías como histogramas, producción de potencia media y producción de “potencia normalizada”. Aunque cada metodología transmite información diferente (útil), las investigaciones adicionales deberían buscar proporcionar una comparación directa de estos métodos.
Se han utilizado varios métodos matemáticos para analizar las respuestas al entrenamiento físico. El uso de modelos de impulso-respuesta ha recibido un apoyo sustancial en la literatura científica, mientras que los enfoques alternativos como el metamodelo PerPot y el modelado lineal mixto aún no han sido completamente explorados. El tipo de análisis que utiliza un investigador/entrenador dependerá de la cantidad de puntos de datos disponibles, y los modelos más complejos requieren que se realicen más mediciones a lo largo del tiempo. Es probable que algunos de los métodos discutidos aquí no aporten información útil para describir la relación
entre entrenamiento y rendimiento. Sin embargo, es probable que alguna combinación de estos métodos, en lugar de un modelo único, nos pueda proporcionar la mejor descripción del complejo fenómeno de las respuestas fisiológicas al entrenamiento.
Referencia Original
Simon A. Jobson, Louis Passfield, Greg Atkinson, Gabor Barton and Philip Scarf. (2009). The Analysis and Utilization of Cycling Training Data. Sports Med. 2009; 39 (10): 833-844 0112-1642/09/0010-0833.
Agradecimientos
La preparación de este manuscrito fue financiada por el Consejo de Investigación en Ingeniería y Ciencias Físicas, Reino Unido. Los autores no tienen conflictos de intereses que sean directamente relevantes para el contenido de esta revisión.
REFERENCIAS
- Godfrey R, Whyte G. Training specificity. In: Whyte G, editor. The physiology of training. London: Churchill Livingstone Elsevier, 2006: 23-43
- Mujika I, Busso T, Lacoste L, et al. Modeled responses to training and taper in competitive swimmers. Med. Sci. Sports Exerc. 1996; 28 (2): 251-8
- Wolfarth B, Bray MS, Hagberg JM, et al. The human gene map for performance and health related fitness phenotypes: the 2004 update. Med. Sci. Sports Exerc. 2005; 37 (6): 881-903
- Banister EW, Calvert TW, Savage MV, et al. A system model of training for athletic performance. Aust. J. Sports Med. 1975; 7: 170-6
- Avalos M, Hellard P, Chatard J-C. Modeling the training- performance relationship using a mixed model in elite swimmers. Med. Sci. Sports Exerc. 2003; 35 (5): 838-46
- Perl J. Modelling dynamic systems: basic aspects and application to performance analysis. Int. J. Comput. Sci. Sport 2004; 3 (2): 19-28
- Foster C, Daniels J, Yarbrough R. Physiological and train- ing correlates of marathon running performance. Aust. J Sports Med. 1977; 9: 58-61
- Foster C, Lehmann M. Overtraining syndrome. In: Guten G, editor. Running injuries. Orlando (FL): WB Saunders, 1997
- Borg G. Borg’s perceived exertion and pain scales. Stockholm: Human Kinetics, 1998: 13
- Singh F, Foster C, Tod D, et al. Monitoring different types of resistance training using session rating of perceived exertion. Int J. Sports Physiol. Perf. 2007; 2 (1): 34-45
- Foster C, Hector LL, Welsh R, et al. Effects of specific versus cross-training on running performance. Eur J Appl Physiol Occup Physiol 1995; 70: 367-72
- Foster C, Florhaug JA, Franklin J, et al. A new approach to monitoring exercise training. J Strength Cond Res 2001; 15 (1): 109-15
- Seiler KS, Kjerland GØ. Quantifying training intensity distribution in elite endurance athletes: is there evidence for an ‘‘optimal’’ distribution? Scand J Med Sci Sports 2006; 16: 49-56
- Calvert TW, Banister EW, Savage MV. A systems model of the effects of training on physicalperformance. IEEE Trans Syst Man Cybern 1976; 6 (2): 94-102
- Rowbottom DG, Keast D, Garcia-Webb P, et al. Training adaptation and biological changes among well-trained male triathletes. Med. Sci. Sports Exerc. 1997; 29 (9): 1233-9
- Achten J, Jeukendrup AE. Heart rate monitoring: applications and limitations. Sports Med 2003; 33 (7): 517-38
- Leweke F, Bruck K, Olschewski H. Temperature effects on ventilatory rate, heart rate, and preferred pedal rate during cycle ergometry. J. Appl. Physiol. 1995; 79 (3): 781-85
- Borresen J, Lambert MI. Changes in heart rate recovery in response to acute changes in training load. Eur. J. Appl. Physiol. 2007; 101: 503-11
- Borresen J, Lambert MI. Autonomic control of heart rate during and after exercise: measurements and implications for monitoring training status. Sports Med. 2008; 38 (8): 633-46
- Taha T, ThomasSG. Systems modelling of the relationship between training and performance. Sports Med 2003; 33 (14): 1061-73
- Banister EW, Calvert TW. Planning for future performance: implications for long term training. Can. J. Appl. Sport Sci. 1980; 5 (3): 170-6
- Morton RH, Fitz-Clarke JR, Banister EW. Modeling human performance in running. J. Appl. Physiol. 1990; 69 (3): 1171-7
- Desgorces FD, Senegas X, Garcia J, et al. Methods to quantify intermittent exercises. Appl Physiol Nutr Metab. 2007; 32 (4): 762-9
- Foster C, Hoyos J, Earnest C, et al. Regulation of energy expenditure during prolonged athletic competition. Med. Sci. Sports Exerc. 2005; 37 (4): 670-5
- Padilla S, Mujika I, Santisteban J, et al. Exercise intensity and load during uphill cycling in professional 3-week races. Eur. J. Appl. Physiol. 2008; 102 (4): 431-8
- Hurley BF, Hagberg JM, Allen WK, et al. Effect of training on blood lactate levels during submaximal exercise. J. Appl. Physiol. 1984; 56 (5): 1260-4
- Rusko HK, Pulkkinen A, Saalasti S, et al. Pre-prediction of EPOC: a tool for monitoring fatigue accumulation duringexercise?. Med. Sci. Sports Exerc 2003; 35 (5 Suppl. 1): S183
- Paton CD, Hopkins WG.Tests of cycling performance. Sports Med 2001; 31 (7): 489-96
- Ebert TR, Martin DT, McDonald W, et al. Power output during women’s World Cup road cycle racing. Eur. J. Appl. Physiol. 2005; 95 (5-6): 529-36
- Ebert TR, Martin DT, Stephens B, et al. Power output during a professional men’s road-cycling tour. Int J Sports Physiol Perf 2006; 1: 324-35
- Jobson SA, Nevill AM, Jeukendrup A. The efficacy of power output measurement during a professional cycle stage race: a case study. J.Sports. Sci 2005; 23 (11-12): 1292
- Theurel J, Lepers R. Neuromuscular fatigue is greaterfol- lowing highly variable versus constant intensity endurance cycling. Eur J Appl Physiol 2008; 103 (4): 461-8
- Palmer GS, Hawley JA, Dennis SC, et al. Heart rate re- sponses during a 4-d cycle race. Med Sci Sports Exerc 1994, 26: 1278-83
- Coggan AR. Training and racing using a power meter: an introduction. Revised 25 March 2003 [online]. Available from URL: http://www.midweekclub.ca/articles/coggan. pdf [Accessed 2008 May 4]
- Skiba P. Evaluation of a novel training metric in trained cyclists.. Med. Sci. Sports Exerc 2007; 39 (Suppl. 5): S448
- Olds TS, Norton KI, Lowe EL, et al. Modeling road-cycling performance. J. Appl. Physiol. 1995; 78 (4): 1596-611
- Hu K, Ivanov PCh, Chen Z, et al. Non-random fluctuations and multi scale dynamics regulation of human activity. Physica A 2004; 337: 307-18
- Terblanche E, Wessels JA, Stewart RI, et al. A computer simulation of free-range exercise in the laboratory. J Appl Physiol 1999; 87 (4): 1386-91
- Tucker R, Bester A, Lambert EV, et al. Non random fluctuations in power output during self-paced exercise. Br. J. Sports Med 2006; 40: 912-7
- Busso T. Variable dose-response relationship between exercise training and performance. Med. Sci .Sports Exerc. 2003; 35: 1188-95
- Morton RH.Modelling training and overtraining. J. Sports Sci. 1997; 15: 335-40
- Busso T, Thomas L. Using mathematical modelling in training planning. Int. J. Sports Physiol. Perf. 2006; 1: 400-5
- Busso T, Carasso C, Lacour JR. Adequacy of a systems structure in the modelling of training effects on performance. J Appl Physiol 1991; 71 (5): 2044-9
- Fitz-Clarke JR, Morton RH, Banister EW. Optimizing athletic performance by influence curves. J Appl Physiol 1991; 71 (3): 1151-8
- Busso T, Candau R, Lacour JR. Fatigue and fitness modelled from the effects of training on performance. Eur. J. Appl. Physiol. 1994; 69 (1): 50-4
- Busso T, Denis C, Bonnefoy R, et al. Modeling of adaptations to physical training by using a recursive least squares algorithm. J. Appl. Physiol. 1997; 82 (5): 1685-93
- Hellard P, Avalos M, Lacoste L, et al. Assessing the limitations of the Banister model in monitoring training. J. Sports Sci. 2006; 24 (5): 509-20
- Edelmann-Nusser J, Hohmann A, Henneberg B. Modeling and prediction of competitive performance in swimming upon neural networks. Eur. J. Sport Sci. 2002; 2: 1-12
- Stevens J. Applied multivariate statistics for the social sci-ences. Hillsdale (NJ): Erlbaum, 1986
- Mujika I, Chatard JC, Busso T, et al. Use of swim training profiles and performance data toenhance training effec- tiveness. J. Swimming Res. 1996; 11: 23-9
- Cnaan A, Laird NM, Slasor P. Using the general linear mixed model to analyse unbalanced repeated measures and longitudinal data. Stat. Med. 1997; 16 (20): 2349-80
- Blackwell E, de Leon CFM, Miller GE. Applying mixed regression models to the analysis of repeated-measures data in psychosomatic medicine. Psychosom. Med. 2006; 68 (6): 870-8
- Li H, Wood CL, Getchell TV, et al. Analysis of oligonucleotide array experiments with repeated measures using mixed models. BMC Bioinformatics 2004; 5: 209
- Piepho HP, Buchse A, Richter C. A mixed modelling ap-proach for randomized experiments with repeated mea- sures. J. Agron. Crop. Sci. 2004; 190 (4): 230-47
- Aguilera R, Becchi M, Casabianca H, et al. Improved method of detection of testosterone abuse by gas chromatography/combustion/isotope ratio mass spectrometry analysis of urinary steroids. J. Mass. Spectrom. 1996; 31 (2): 169-76
- Ball KA, Best RJ. Different centre of pressure patterns within the golf stroke, I: cluster analysis. J. Sports Sci. 2007; 25 (7): 757-70
- Perkiomaki JS, Makikallio TH, Huikuri HV. Fractal and complexity measures of heart rate variability. Clin. Exp. Hypertens. 2005; 27 (2-3): 149-58
- Briggs J. Fractals: the patterns of chaos. New York: Simon & Schuster Inc., 1992
- Ward M. Beyond chaos: the underlying theory behind life, the universe and everything. New York: St. Martin’s Press, 2001
- Guevara MR, Glass L, Schrier A. Phase locking, period doubling bifurcations, and irregular dynamics in periodi- cally stimulated cardiac cells. Science 1981; 214: 1350-3
- Padmanabhan V, Semmlow JL. Dynamical analysis of diastolic heart sounds associated with coronary artery disease. Ann. Biomed Eng. 1994; 22 (3): 264-71
- Skinner JE, Molnar M, Vybiral T, et al. Application of chaos theory to biology and medicine. Integr. Physiol. Behav. Sci. 1992; 27 (1): 39-53
- St Clair Gibson A, Goedecke JH, Harley YX, et al. Meta-bolic set point control mechanisms in different physiological systems at rest and during exercise. J Theor. Biol. 2005; 236: 60-72
- Chamchad D, Djaiani G, Jung HJ, et al. Nonlinear heart rate variability analysis may predict atrial fibrillation after coronary artery bypass grafting. Anesth Analg 2006; 103 (5): 1109-12
- Saeed M. Fractals analysis of cardiac arrhythmias. Sci.World. J. 2005; 5: 691-701